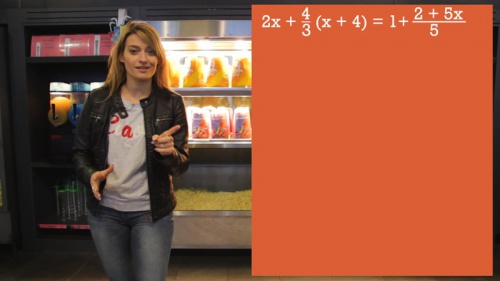Wiskunde 1ste graad A
Vergelijkingen en vraagstukken 1ste graad A
Vergelijkingen en vraagstukken oplossen wordt wel eens het moeilijkste binnen de getallenleer genoemd! Dankzij deze reeks video's met Bart wordt dit voor jou een hapje en los zelfs jij binnenkort de moeilijkste vergelijkingen en vraagstukken op! Wiskunde wordt easy!
Liesbeth legt uit hoe we tewerk gaan met een vergelijking van 1ste graad. (1ste graad)
Liesbeth gaat een vraagstuk met een eerstegraadsvergelijking oplossen in vier stappen. (1ste graad)
Liesbeth lost in de bioscoopzaal een vraagstuk op met een eerste graadsvergelijking. (1ste graad)
Vergelijkingen en vraagstukken
Veel leerlingen van de eerste graad vinden vergelijkingen en vraagstukken het allermoeilijkste onderdeel van getallenleer en van wiskunde in het algemeen. Vind jij dat ook? Dan hebben we goed en slecht nieuws voor jou. Eerst het slechte nieuws: vergelijkingen en vraagstukken zijn heel belangrijk want de principes komen terug in heel wat andere wetenschappelijke vakken. Het goede nieuws is: we leggen je heel eenvoudig uit hoe je vergelijkingen en vraagstukken kan oplossen. Niet met saaie stukken theorie maar met leuke online lesvideo’s en duidelijke voorbeelden.
Vergelijkingen oplossen
Een vergelijking oplossen lijkt moeilijk, maar bij WeZooz Academy leggen we het je simpel uit. Onze enthousiaste leerkracht/entertainer, Bart, laat je aan de hand van een simpel stappenplan zien hoe je een vergelijking van de eerste graad, ook wel een eerstegraadsvergelijking of eerstegraadsfunctie genoemd, snel kan oplossen. In vijf eenvoudige stappen legt hij uit hoe je een eerstegraadsvergelijking uitrekent en de waarde van de onbekende (meestal ‘x’ genoemd) berekent.
Eerstegraadsvergelijking oplossen: 5 simpele stappen
1. Haakjes uitwerken volgens de regenregels, de volgorde en de eigenschappen van bewerkingen.
2. Breuken: elke term op dezelfde noemer zetten zodat die noemers daarna geschrapt kunnen worden.
3. Alle termen met de onbekende naar het linkerlid brengen, alle andere termen naar het rechterlid.
4. Reken het linkerlid en het rechterlid uit.
5. Deel beide leden door de coëfficiënt van de term met de onbekende.
Vraagstukken oplossen
Je vraagt je misschien af: een eerstegraadsfunctie kunnen uitrekenen, waarom heb ik dat nu nodig?! Wel, om vraagstukken te kunnen oplossen. En om dat te kunnen, met je altijd beginnen met het lezen van de vraag. Heel aandachtig zodat je zeker niets over het hoofd ziet. Vraagstukken uit de wiskunde kan je noteren als een vergelijking van de eerste graad. Dat waar naar gevraagd wordt in het vraagstuk is de onbekende (= x). De andere gegevens in de opgave kan je gebruiken om deze onbekende te vinden.
Vraagstukken oplossen in 4 stappen
Een vraagstuk oplossen, kan je in vier stappen.
1. Zoek de onbekende en noem deze ‘x’.
2. Stel de eerstegraadsvergelijking op door gebruik te maken van alle nuttige gegevens in de opgave.
3. Los de eerstegraadsfunctie op door gebruik te maken van de vijf stappen (zie hierboven).
4. Schrijf de antwoordzin op.
Controleer altijd je oplossing
Als je een vraagstuk hebt opgelost en je de antwoordzin netjes hebt uitgeschreven, is er eigenlijk nog iets wat je moet doen. Je oplossing controleren. Hoe doe je dit? Heel simpel, door je oplossing (= het gevonden getal) in te vullen in de eerstegraadsvergelijking en te controleren of het klopt. Zo ben je zeker dat je antwoord juist is en scoor je gemakkelijk tien op tien!