Wiskunde 1ste graad A
Natuurlijke (##NN##) en Gehele (##ZZ##) getallen
- Inhoudstafel
- Verzameling N en Z: definities en voorstellingen!
- Verzameling ##NN## en ##ZZ## definities en voorstellingen: Oefeningen
- Verband tussen N en Z
- Verband tussen ##NN## en ##ZZ##: Oefeningen
- N en Z voorstellen op de getallenas!
- ##NN## en ##ZZ## voorstellen op de getallenas: Oefeningen
- N en Z in het assenstelsel!
- ##NN## en ##ZZ## in het assenstelsel: Oefeningen
- Ordenen van N en Z (onderling vergelijken)!
- Ordenen van ##NN## en ##ZZ## (onderling vergelijken): Oefeningen
- TEST - Natuurlijke (##NN##) en Gehele (##ZZ##) getallen
Natuurlijke (##NN##) en Gehele (##ZZ##) getallen
Lestraject bekijken?
Probeer WeZooz Academy meteen even GRATIS uit en start met leren dankzij onze diverse lestrajecten voor vakken in de 1ste graad A!
In dit lestraject leer je over de natuurlijke (N) en de gehele (Z) getallen.
Welke getallen zijn dit juist? Wat is het onderlinge verband? Hoe stel je deze getallen voor op een getallenas en hoe kan je ze onderling vergelijken?
Dit
lestraject bestaat uit 11 lessen,
Geschatte duurtijd: 25 minuten.
- Inhoudstafel Natuurlijke (##NN##) en Gehele (##ZZ##) getallen
-
Verzameling N en Z: definities en voorstellingen!
-
Verzameling ##NN## en ##ZZ## definities en voorstellingen: Oefeningen
-
Verband tussen N en Z
-
Verband tussen ##NN## en ##ZZ##: Oefeningen
-
N en Z voorstellen op de getallenas!
-
##NN## en ##ZZ## voorstellen op de getallenas: Oefeningen
-
N en Z in het assenstelsel!
-
##NN## en ##ZZ## in het assenstelsel: Oefeningen
-
Ordenen van N en Z (onderling vergelijken)!
-
Ordenen van ##NN## en ##ZZ## (onderling vergelijken): Oefeningen
-
TEST - Natuurlijke (##NN##) en Gehele (##ZZ##) getallen


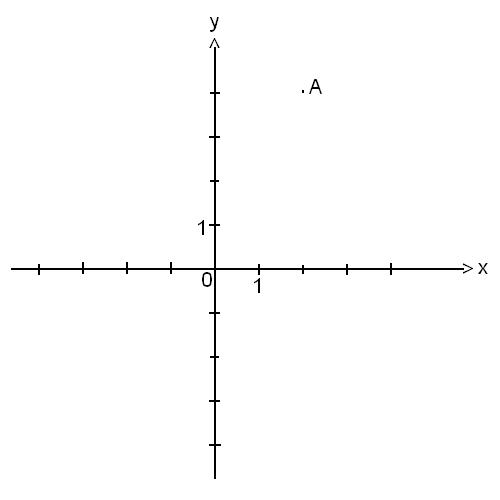 Kies een antwoord uit de lijst.
Kies een antwoord uit de lijst.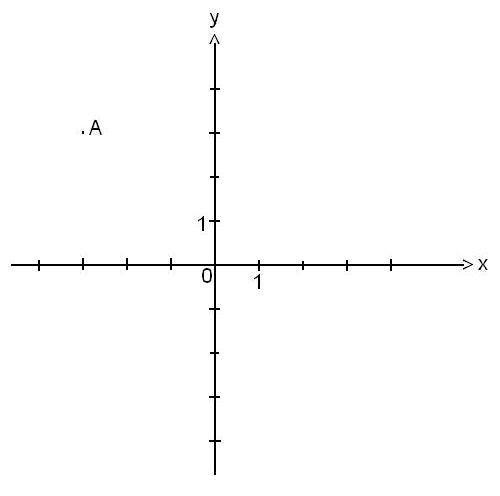 Kies een antwoord uit de lijst.
Kies een antwoord uit de lijst.