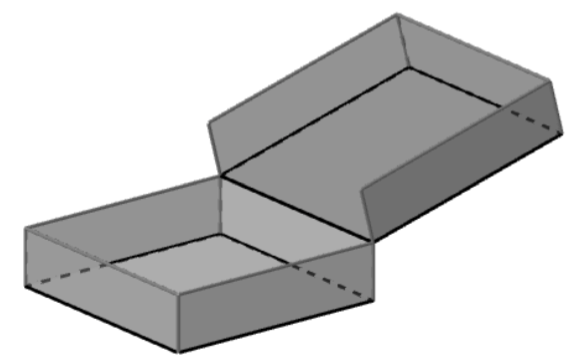
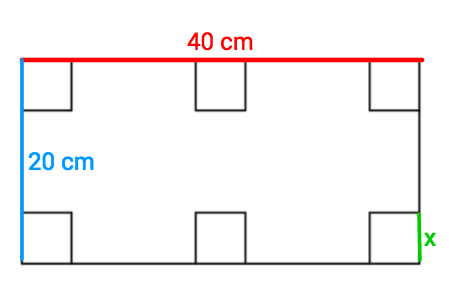
Afgeleiden 6: Verloop
Lestraject bekijken?
Probeer WeZooz Academy meteen even GRATIS uit en start met leren dankzij onze diverse lestrajecten voor vakken in de 3de graad!
Dit traject bevat twee video's over hoe je met behulp van afgeleiden, de minima en de maxima van een functie kan berekenen. Je kan ook een toepassing uit de economie uitgewerken als oefening. Op het einde kan je jezelf testen met een toets. Veel succes!
Dit
lestraject bestaat uit 5 lessen,
Geschatte duurtijd: 13 minuten.
 Leraar:
Leraar: