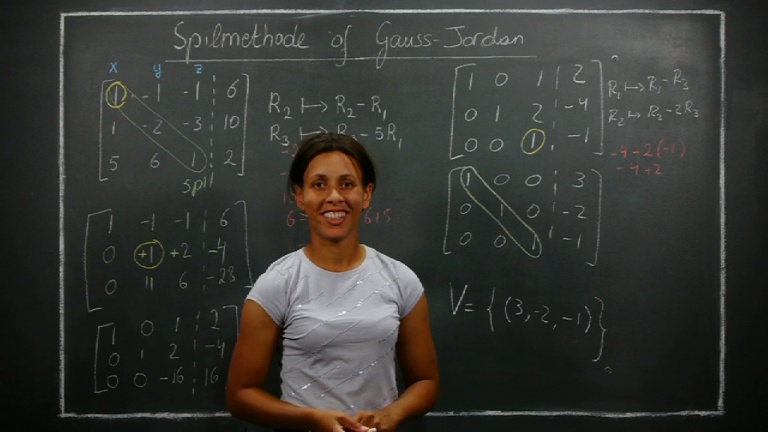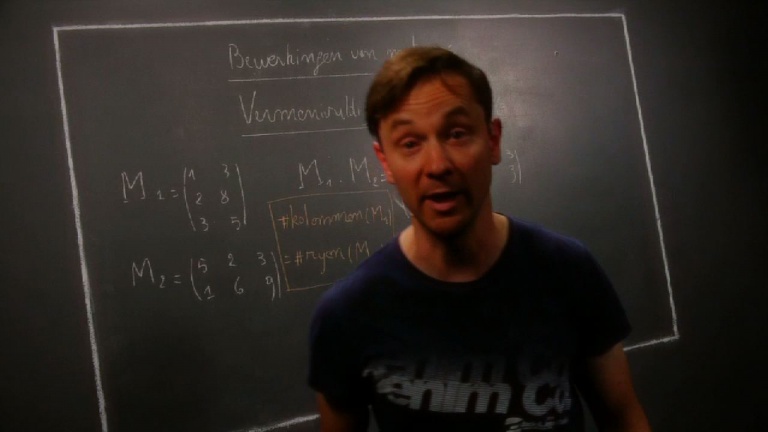Zoeken naar "stelsels"
Lestrajecten
Stelsels oplossen - Deel 1
In dit traject leer je 2 methodes om stelsels op te lossen:
- Stelsels van 2 eerstegraadsvergelijkingen grafisch oplossen
- Stelsels van 2 eerstegraadsvergelijkingen oplossen met de substitutiemethode
Stelsels oplossen - Deel 2
Je kent al 2 methodes voor het oplossen van stelsels. In dit traject leer je er nog 2:
- Stelsels van 2 eerstegraadsvergelijkingen oplossen met de combinatiemethode
- Stelsels van 2 eerstegraadsvergelijkingen oplossen met de combinatie-puurmethode
Stelsels oplossen - Deel 3: Vraagstukken
Leer hier vraagstukken oplossen aan de hand van stelsels. Onze leerkracht begeleidt je met 3 voorbeelden!
Stelsels en matrices 1: Stelsel voorstellen door een matrix
In dit eerste traject over stelsels en matrices kan je één video bekijken waarin een stelsel van vergelijkingen omgezet wordt naar een matrix. Je leert wat de coëfficiëntenmatrix is en de uitgebreide matrix. Dus er wordt wel verwacht dat je de basis van matrices al goed kent.
Maak daarna de oefening en test jezelf op het einde! Veel succes!
Stelsels en matrices 3: De Gauss-Jordan-methode - Extra oefeningen
Dit traject bevat 2 uitgewerkte oefeningen over de Gauss-Jordan-methode of de spilmethode voor het oplossen van een stelsel van vergelijkingen. Maak op het einde de test en kijk of als goed begrepen hebt! Veel succes!
Stelsels en matrices 2: De Gauss-Jordan-methode
Dit traject toont hoe je de Gauss-Jordan-methode of spilmethode kunt toepassen om een stelsel op te lossen.
Het bevat twee video's, eentje met de volledige uitleg over Gauss-Jordan, de andere met korte uitgewerkte oefening.
Doe op het einde de toets en test jezelf!
Werken met matrices 1: Opstellen, optellen en vermenigvuldigen met een constante
In dit traject leer je de basis van werken met matrices. Er wordt uitgelegd hoe je een matrix moet opstellen en hoe je een stelsel kan omzetten naar de matrix. Je leert ook hoe je een matrices met elkaar optelt en hoe je een matrix vermenigvuldigt met een reëel getal.
Werken met matrices 3: Transponeren en eigenschappen van matrixbewerkingen
Dit traject overloopt de eigenschappen van de bewerkingen met matrices. Je moet al wel bekend zijn met het optellen en vermenigvuldigen van matrices. Dit traject bespreekt hoe het zit met de commutativiteit, associativiteit en distributiviteit van die bewerkingen.
In dit traject leer je ook hoe je een matrix transponeert. Veel succes!
Werken met matrices 2: Matrices vermenigvuldigen en machten van een matrix
In dit traject leer je meer over matrixbewerkingen. Hoe moet je matrices met elkaar te vermenigvuldigen en ook hoe je een matrix tot een macht moet verheffen? Je moet dus al bekend zijn met matrices en hoe je deze moet opstellen.
Maak de oefeningen, doe op het einde de test en zie of je alles goed begrepen hebt!