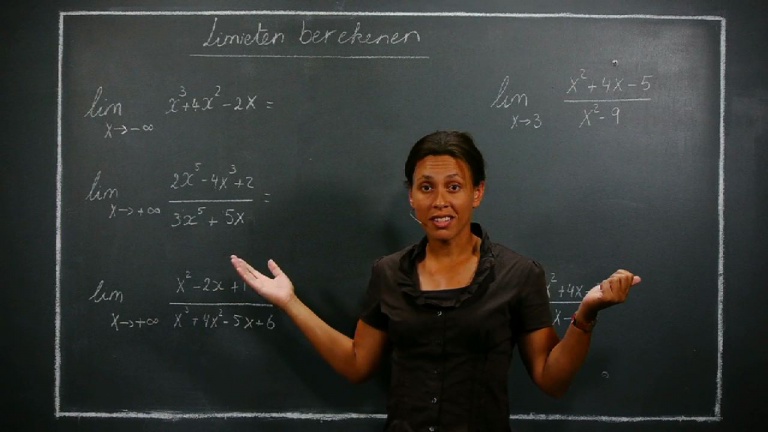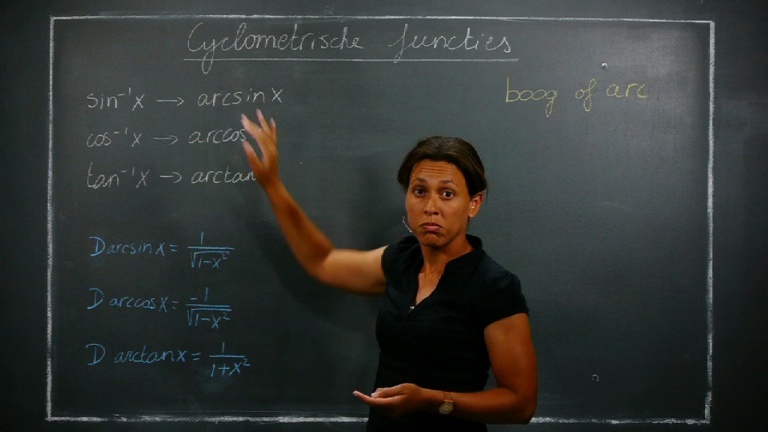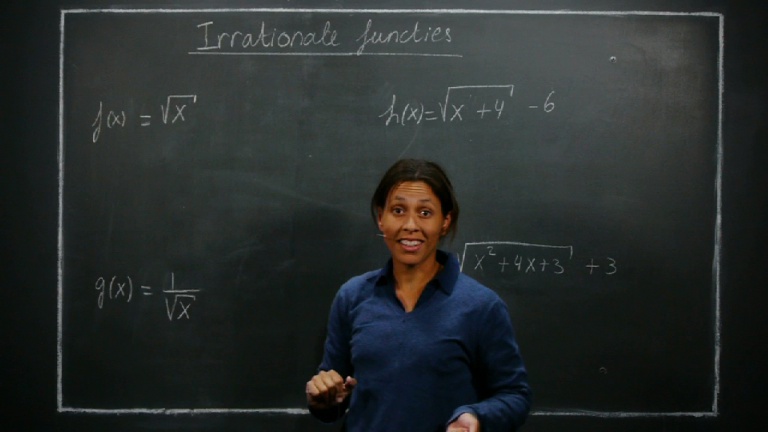Zoeken naar "welke"

Dit traject bevat twee video's waarin je limieten leert berekenen. De grafiek van de functie wordt dus niet gegeven. De limiet in een bepaalde waarde vertelt ons naar welke beeldwaarde de grafiek steeds meer nadert. We zullen ook het onderscheid maken tussen de limiet in een bepaalde waarde en de limiet in oneindig.

Je komt alles te weten over bijzinnen, en ontdekt ook wat het verschil is tussen een bijwoordelijke bijzin en een betrekkelijke bijzin! Verder zal je twee soorten bijwoordelijke bijzinnen (adverbial clauses) leren kennen: de adverbial clause of time en de adverbial clause of reason.

Een cyclometrische functie is de inverse functie van een goniometrische functie. Dit traject bevat één video over cyclometrische functies en geeft uitleg hoe je een cyclometrische functie moet oplossen en welke voorwaarden je moet stellen. Je krijgt ook te zien wat de afgeleiden zijn van de cyclometrische functies.

Wat de samengestelde tijden zijn? Euhm... Tijden die werden samengesteld zeker? Is de passé composé niet zo'n geval?!
Inderdaad ja. De samengestelde tijden bestaan telkens uit een "auxiliaire" of hulpwerkwoord en een "participe passé" of voltooid deelwoord. 

Wanneer kies je nu welk hulpwerkwoord en welke andere samengestelde tijden bestaan er? 
Dit kom je allemaal te weten door de twee video's te bekijken. 

Veel succes! 

Irrationale functies zijn functies waarbij de x onder een wortel staat. Daarom moet je goed opletten welke waarden voor x je invult in de functie. Er zullen bepaalde waardes uitgesloten worden. Ook het berekenen van de nulpunten van een irractionale functie vraagt iets meer stappen dan bij een gewone veelterm functie.

Dit traject bevat twee video's over hoe je het domein en de nulpunten van een irrationale functie moet bepalen.