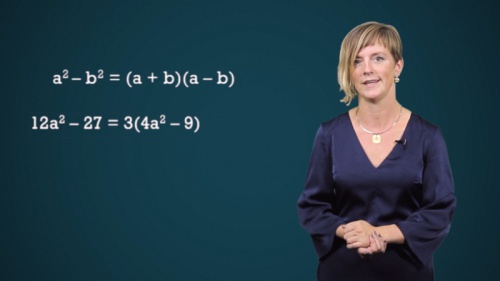Wiskunde 2de graad
Getallenleer 2de graad
De briljante lesvideo’s die je in deze categorie ‘getallenleer’ kan bekijken, behandelen stuk voor stuk onderdelen uit de wiskundige onderzoeksdomeinen getallenleer en algebra. Wiskunde is –zoals jij ondertussen al wel weet- veel meer dan gewoon een beetje lukraak rekenen met gegeven cijfermateriaal…
Er zijn in de wiskunde ook wel degelijk bepaalde regels die je gevolgd moeten worden als je aan het rekenen wil slaan. Dat zijn onder andere dingen die je leert in deze reeks videolessen.
Het zijn de coole Sjoert en de poeslieve Tine die jou van de nodige wiskundekennis gaan voorzien om in het dagelijkse leven te kunnen rekenen met allerhande getallen, letters en grootheden. Zelfs als je al een held bent in het rekenen, durf ik ervoor te wedden dat je toch nog wat zal bijleren.
Do I smell a bet ;-)?
Nu goed, Tine en Sjoert zijn er klaar voor! Jij ook? Alright!
“Getallenleer, algebra, rekenen, wiskunde? Pfuh, da’s een eitje!”
Annelies verdiept zich in het opstellen van rijen. (tweede graad)
Annelies maakt oefeningen op de meetkundige rij. (tweede graad)
Annelies maakt oefeningen op de rekenkundige rij. (tweede graad)
Annelies legt je in deze lesvideo getallenleer uit wat een meetkundige rij is. (tweede graad)
Sjoert laat je in deze video zien hoe je de som van de eerste n-termen neemt van een meetkundige rij. (tweede graad)
Sjoert laat je in deze getallenleervideo zien hoe je de som van een rekenkundige rij neemt. (tweede graad)
Annelies vertelt je in deze lesvideo wat een rekenkundige rij in de getallenleer juist is. (tweede graad)
Sjoert laat je kennis maken met de rij van Fibonacci in de wiskunde. (tweede graad)
Annelies geeft in deze lesvideo een inleiding op ontbinden in factoren is. (2de graad)
Annelies legt in deze lesvideo uit hoe je gemeenschappelijke factoren voorop zet. (2de graad)
Annelies laat in deze lesvideo zien hoe je termen telt. (2de graad)
Annelies ontbindt in deze lesvideo wiskunde het verschil van 2 kwadraten. (2de graad)
Getallenleer is zoals eten: belangrijk
Wiskunde zonder getallen is zoals een café zonder bier of zoals cola zonder prik. Het bestaat gewoonweg niet of het is in ieder geval zeer vreemd. Het onderzoeken van de eigenschappen van getallen heet in de wiskunde getallenleer. In de eerst graad maakte je al kennis met de basiseigenschappen van getallen zoals natuurlijke en gehele getallen. In de tweede graad gaan we nog een stapje verder. We dompelen ons dus nog iets dieper in die magische oceaan van getallenleer. Met de lesvideo’s van WeZooz Academy is het een kwestie van tijd vooraleer dit klaar en duidelijk is.
Nog meer getallenleer?
Je herinnert je ongetwijfeld de lessen getallenleer van de eerste graad nog. Veel van die leerstof zie je, in een iets complexere vorm, terug in de tweede graad. Betekent dit dan moeilijkere leerstof? ABSOLUUT NIET! De lesvideo’s van WeZooz Academy tonen aan dat getallen fijn en leuk zijn om mee te rekenen. Samen met de leerkracht wiskunde ontdek je dit snel!
Ontbinden in factoren?! Hoe ging dat weeral?
Het eerste leerstofonderdeel van getallenleer dat al direct een lampje zal doen branden is het ontbinden in factoren of zoals de definitie het zegt: “Het opnieuw uitschrijven van veeltermen als een product.”. In de eerste graad werd voornamelijk de basis behandeld. In de tweede graad gaan we een stapje verder. Samen met leerkracht Sjoert zal het snel duidelijk en eenvoudig zijn. Stap voor stap zodat je niets belangrijk vergeet. Voorbereiding, het echte werk en extra oefeningen. Niets wordt aan het toeval overgelaten. Het lijkt alsof je nooit iets anders gedaan hebt. Daarnaast behandelt Sjoert ook het algoritme van Horner.
Rationale getallen
“Rationale getallen waren dat nu enkel breuken of ook natuurlijke, gehele en decimale getallen?” Geen enkel probleem als dit even uit je geheugen is ontsnapt. Het antwoord is dat zowel natuurlijke als gehele getallen ook rationale getallen zijn. In twee gevallen behoren ook decimale getallen tot de groep van de rationale getallen. Kort omschreven zijn rationale getallen breuken.
In de tweede graad ligt de focus bij rationale getallen bij het omzetten van breuken naar decimale getallen en omgekeerd. Want zoals je al wel kon afleiden zijn rationale getallen ook decimale getallen. Omgekeerd niet altijd!
Reële getallen
Nog een stapje verder dan de rationale getallen zijn de reële getallen. Deze groep uit de getallenleer bevat naast de rationale getallen ook irrationale getallen. Klinkt allemaal nogal verwarrend en onduidelijk, niet? Volstrekt te begrijpen. Met de lesvideo’s wiskunde van WeZooz Academy is dat binnenkort verleden tijd.
Kort samengevat zijn de reële getallen een groep die je kan opsplitsen in twee groepen. Zoals eerder gezegd de rationale en irrationale getallen. De rationale getallen zijn al eerder beschreven hierboven. De irrationale getallen gaan nog een stapje verder. Het is een reëel getal dat niet te schrijven is als quotiënt van twee gehele getallen, een vierkantswortel bijvoorbeeld. Het berekenen van een vierkantswortel behoort dan ook tot dit leerstofonderdeel. Daarnaast worden ook de priemgetallen en intervallen behandeld.
Benieuwd naar de lesvideo’s? Laat je gaan en denk eraan: LOL = Learning On-Line!
Populaire lestrajecten getallenleer:
· REËLE GETALLEN - KENNISMAKEN EN REKENEN MET VIERKANTSWORTELS
· REËLE GETALLEN – PRIEMGETALLEN
· REËLE GETALLEN - INTERVALLEN